Introducing Miscreant: a multi-language misuse resistant encryption library

For the past several months I have been hacking on not just one, but five encryption libraries in five different languages (Go, Python, Ruby, Rust, and TypeScript). Tall order, I know. And worse, these libraries implement what I believe is a novel cryptographic construction. Are you terrified yet? Yes, I’m implementing novel cryptography, in several languages at that, but I’d like to convince you it’s not as scary as it sounds.

Why? Because I’m implementing algorithms originally created by a cryptographer, Phil Rogaway, whose decades of work is just starting to receive the mainstream attention it deserves. These algorithms are extremely simple and designed to be easy-to-implement. Finally, they’re all built atop otherwise standard AES modes.

The library is Miscreant, and it’s available on GitHub in the form of a multi-language monorepo at:

https://github.com/miscreant/miscreant

The Problem: Nonce Reuse #

The recent KRACK Attacks have demonstrated a problem in practice which Miscreant aims to solve strategically: all of the cryptographic ciphers we use in practice today fail catastrophically when nonces are reused.

If you didn’t happen to hear about the KRACK Attacks, they are nonce reuse attacks against WPA2, a protocol which is considered the state-of-the-art in WiFi encryption. Depending on the exact WPA2 configuration used, and with an attacker in physical proximity, KRACK can recover plaintext traffic, or for ciphers which fail particularly catastrophically (i.e. AES-GCM), KRACK can enable traffic forgeries, i.e. enabling the attacker impersonating an access point.

Is Miscreant a magical solution to the KRACKs of the world? Probably not. Cryptography is complicated, and rarely is a new cryptography library (or in Miscreant’s case, set of libraries) a magical panacea for a problem that occurs around the time it’s announced. Miscreant’s solution to this particular problem comes at a price: a performance penalty, at least for encryption. Does it make sense for WiFi? Only time will tell… we’ll see but perhaps not.

That said, nonce reuse abounds elsewhere beyond KRACK, particularly anywhere users of cryptography libraries are asked to choose their own nonces. Miscreant can provide a defense in these cases: data-at-rest encryption, encrypting keys with other encryption keys, large file encryption, and even online protocols.

How you ask? Let’s look at what Miscreant provides.

The Solution: Misuse Resistance #

Miscreant implements two modes of AES which provide a unique property called “nonce reuse misuse resistance”. But to understand what that is, I first need to describe a nonce.

A nonce (which is somewhat analogous to an initialization vector, if you’re familiar with those) is a single-use value which enables securely encrypting multiple messages under the same key. Nonces need not be random: we can use a counter, so long as the values are never repeated under the same key.

Repeated use of the same nonce under the same key causes most ciphers to fail catastrophically, as we just saw with the recent KRACK attack. If you repeat a nonce under AES-GCM, possibly the most popular authenticated mode of AES and otherwise a fairly good mode, you can XOR together two ciphertexts produced under the same key/nonce and the keystream will cancel out, leaving the XOR of the two plaintexts.

But even worse, repeating a nonce under AES-GCM leaks the cipher’s authentication key, allowing an attacker to perpetrate chosen ciphertext attacks including message forgeries and even potentially full plaintext recovery. The XSalsa20Poly1305 and ChaCha20Poly1305 constructions, found in NaCl-family libraries such as libsodium, fail in a similarly spectacular way (despite these libraries often being described as “misuse resistant”).

As an author of one of the earliest bindings to NaCl/libsodium, I’ve long felt unsatisfied with this state of affairs. As I authored documentation for that library, I included the following rather unsatisfying caveats on the library’s usage:

• What the algorithm does for you: ensures data is kept confidential and that it cannot be undetectably modified by an attacker
• What the algorithm expects from you: a secret key which must be kept confidential, and a unique (“nonce”) value each time the SecretBox function is used. The SecretBox function must never ever be called with the same key/nonce pair!
• What happens if you reuse a nonce: ALL IS LOST! complete loss of the confidentiality of your data (provided nonces are reused with the same key). Do NOT let this happen or you are breaking the security of your system.

I really wished the underlying algorithm was more robust so this entire category of cryptographic failure simply wasn’t possible.

I’m certainly not alone: nonce reuse misuse resistance has been an unspoken theme of the CAESAR competition to develop next-generation authenticated encryption ciphers. Google has also been working on standardizing a very fast algorithm called AES-GCM-SIV with slightly weaker security properties (self-described by Adam Langley as “occasional nonce duplication tolerant”) through the IRTF.

If others, including renowned cryptographers, are working on this same problem, why Miscreant then? I have been primarily attracted to the simplicity of the algorithms it implements. The entries to the CAESAR competition, along with Google’s proposed standard (AES-GCM-SIV), are all quite fast but rather complicated.

For example, during last call AES-GCM-SIV has received two proposals for major changes (one to replace the custom “POLYVAL” function with the “GHASH” function used by AES-GCM, and another to redo the key derivation scheme yet again for better performance). This was all after a previous round of fixes after the NSA discovered multiple key recovery attacks. I’m sure a finalized AES-GCM-SIV will wind up being quite fast, and with good security bounds, but with a complicated specification and implementation which is taking quite awhile to get right.

AES-GCM-SIV relies on special CPU instructions, such as the CLMUL instruction, to accelerate the POLYVAL calculation, making it rather slow in environments that do not have similar hardware acceleration for this algorithm, such as mobile clients or embedded/IoT devices. AES-GCM mode is likewise unpopular in the embedded/IoT space for these same reasons, with modes like AES-CCM (also implicated in the recent “KRACK” attacks) generally preferred instead. It sure would be nice if we had a misuse resistant cipher mode which is fast both on servers and on embedded/IoT devices.

Miscreant implements two algorithms, one of which has been sitting nearly unused on the shelf despite having a nearly decade old RFC, and another that’s a new combination of cryptographic primitives with interesting properties. These algorithms are fast anywhere AES is fast, and do not rely on Intel-specific instructions for performance, making them much more applicable to things like the embedded/IoT space than AES-GCM-SIV. Furthermore, the code size is much smaller, and among the smallest you will find for an algorithm with misuse resistance.

These algorithms are AES-SIV and AES-PMAC-SIV, and I will describe how they work below. For more on nonce reuse misuse resistance, please see the blog post “Nonce misuse resistance 101” by Laurens Van Houtven (lvh).

AES-SIV: AES with a synthetic initialization vector #

Synthetic Initialization Vector, or SIV, is a block cipher mode of operation that derives the initialization vector by computing a Message Authentication Code, or MAC, of the plaintext, along with a set of optional message headers. While this might sound suspiciously like the “MAC-then-encrypt” construction we’ve been warned not to use due to potential padding oracles, the AES-SIV construction uses CTR mode which is not subject to padding oracles, and by encrypting data under the MAC ensures there is a strong cryptographic binding between the MAC of the plaintext and the ciphertext.

AES-SIV was (along with the rest of the algorithms implemented in Miscreant) designed by cryptographer Phil Rogaway and described in RFC 5297 in 2008. Though originally intended to solve the key wrapping problem, i.e. encrypting a key under another key (my original motivation for Miscreant), the SIV construction is designed to support a set of message headers, or “associated data”, one of which can be a nonce. This makes SIV modes generally useful for nonce-based encryption, where deriving an initialization vector from the combination of a nonce a message, and optional associated data provides the nonce reuse misuse resistance property.

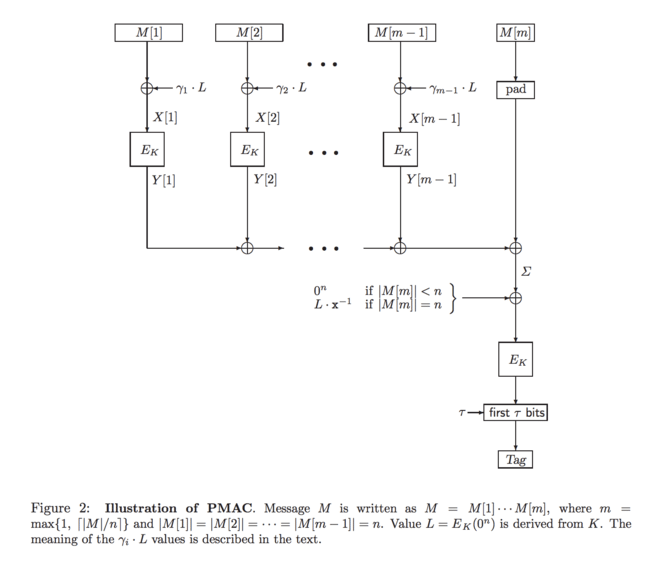
AES-SIV was originally specified using CMAC (and therefore might be more aptly described as AES-CMAC-SIV), a function which turns a block cipher i.e. AES into a message authentication code. CMAC is a secure pseudorandom function (i.e. a keyed hash), and fixes many of the problems of its similar predecessors like CBC-MAC, but it has one particularly notable drawback: it breaks the message into blocks and, much like AES-CBC mode, uses the output ciphertext of the previous block as an input to the next block. This makes CMAC inherently sequential, whereas modes like AES-GCM (as well as AES-GCM-SIV) are fully parallelizable.

This is fine for AES-SIV’s original intended use case, which is the “key wrap” problem of encrypting other encryption keys. However, it makes AES-SIV comparatively slow on modern Intel CPUs when encrypting longer messages. These CPUs are capable of pipelining AES operations, executing as many as 8 of them in parallel, which provides the effective throughput of one AES round per cycle (with an 8 cycle latency, or I believe 4 cycle latency on newer CPUs):

Executing AES as a sort of multi-block batch operation like this is not limited exclusively to Intel CPUs. One of the IoT devices I have been playing with, a Hail, also provides a batch API for performing AES.

Therefore, it’s important for modern schemes to execute in parallel. Fortunately, there is a parallelizable construction quite similar to CMAC which provides the same security properties which we can use instead: PMAC.

AES-PMAC-SIV: AES-SIV with a Parallelizable MAC #

PMAC is a simple cipher-based MAC which can operate in parallel, because unlike CMAC’s sequential chaining of outputs to inputs the MAC is computed by XORing together encryptions of the message, then encrypting the resulting block. It’s a bit trickier than that though: if we did this naively, then if any two blocks ever repeated they’d cancel each other out when XORed together. So PMAC includes a special tweak/offset to each block: a value derived from the key which is XORed into the input block before encrypting, and is never repeated. This ensures all blocks will be unique, even if the ciphertext is repeated.

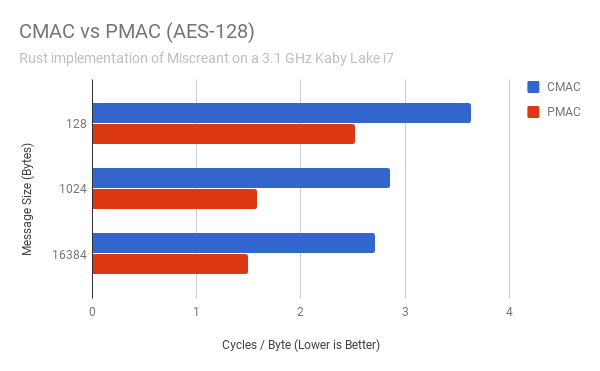
PMAC, when implemented in conjunction with the AES-NI parallelization technique described above, gets great performance in comparison to CMAC. The chart below is a rough benchmark of the relative performance of Miscreant’s Rust implementation of AES-CMAC and AES-PMAC (more on how these are implemented below):

Both of these algorithms exhibit higher performance with larger messages, but it’s interesting to note that the PMAC implementation beats CMAC across the board, regardless of message size.

If PMAC is so great, why is it so obscure? One reason may be patents. PMAC was originally patented by its creator Phil Rogaway, but he has since abandoned his patent filings and states that he knows of no other patents besides his which are applicable to PMAC.

For a full AES-PMAC-SIV construction, we swap CMAC for PMAC, leaving the rest of the construction otherwise unchanged. Is it okay to do to this? Are CMAC and PMAC effectively fungible? I asked Phil Rogaway if this is the case and of all of the proofs from the original AES-SIV paper still hold with PMAC in CMAC’s place. This is what he had to say:

Yes. The proof in the SIV paper uses generic properties of the SIV construction: you can stick in any provably-sound PRF. Quantitative results will depend on the quality of the PRF, but in the case of CMAC and PMAC, the ‘basic’ bounds are the same (within a small constant). I remember there being somewhat improved bounds for PMAC, like [Nandi, Mandal 2007], but by the time you throw in CTR, it probably doesn’t help. So, yes, effectively equivalent, as far as I know.

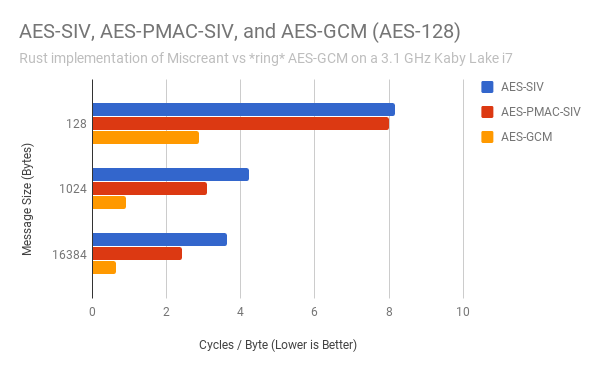
Here is a chart of a run of “cargo bench” showing how the pure Rust implementations of AES-SIV and AES-PMAC-SIV compared to an optimized assembly implementation of AES-GCM found in ring, a Rust crypto library with cipher implementations from BoringSSL (itself an OpenSSL fork):

This is a bit of an apples-to-oranges comparison that works against my favor: I’m comparing a highly optimized implementation of AES-GCM to barely optimized safe Rust code. However, there’s still a lot of low-hanging fruit for future optimizations while keeping the code otherwise pure safe Rust. I am presently looking at moving to a faster Rust-based AES-CTR implementation based off of Intel’s implementation, and there is still considerable low hanging fruit for optimization in the AES-PMAC implementation.

What would the performance of an assembly-optimized AES-PMAC-SIV look like? Rogaway estimates it would perform at ~1.25 cycles/byte, or roughly half the speed of AES-GCM. On my 3.1GHz i7, these numbers translate to AES-PMAC-SIV topping out at ~1.3 GB/sec on a single CPU core, which I think is sufficiently fast to keep encryption from being the bottleneck in most cases.

I wanted to include AES-GCM-SIV for comparison in these charts, unfortunately it’s a moving target as the draft evolves and implementations are hard to come by (all of these are out of date per the latest specs). According to Adam Langley the encryption performance of AES-GCM-SIV is roughly 80% that of AES-GCM (which ballparks at approximately 0.8 cycles/byte), with zero-cost decryption versus AES-GCM. If that’s actually the case, an optimized AES-PMAC-SIV should be ~65% slower than AES-GCM-SIV on modern Intel CPUs. However, AES-PMAC-SIV should be much faster (over twice as fast, as a handwaving, hardware-independent guestimate) on embedded/IoT devices that lack something like a CLMUL instruction.

A Word of Warning #

To my knowledge I’m the only person who has ever implemented the AES-PMAC-SIV construction, and that’s a bit scary (if you know of prior art, please get in touch with me as I’d love to hear about it). I have had to generate my own test vectors which now match across five implementations in five different languages.

All of the Miscreant libraries are presently at version 0.2. I would consider this a pretty early version number for a cryptography library, and one which should give you pause to consider whether these implementations are mature enough to be using yet.

Parts of Miscreant, including some simple finite field arithmetic, are implemented directly in the respective languages supported by the libraries. Depending on which particular language you’re talking about and exactly how it implements integers, there can be concerns around whether it is even possible to implement constant time code in those languages, which is necessary for secure cryptography.

Some next steps are to make the Rust backend accessible in all languages, using bindings like Neon and Helix, but right now the Rust backend requires the nightly compiler and only works on x86.

The Key Wrap Problem (and the “Key Rap”) #

When I started Miscreant it was to solve a very particular problem known as key wrapping. The idea of key wrapping is pretty simple: we just want to encrypt an encryption key with another encryption key. This same idea can be applied in some other contexts besides just keys: credentials, particularly ones that include some sort of random identifier, are a great use case for key wrapping.

SIV modes let us do something pretty neat when encrypting another encryption key: we can omit the nonce entirely. Encrypting an AES-128 key (or 128-bit random identifier ala a UUID) can be done safely using a 32-byte (i.e. 256-bit) message. This is the smallest message payload achievable for this use case while still providing authenticated encryption.

I think key wrapping and credential encryption are two particularly interesting use cases for Miscreant, and something I’d like to explore in the future is using Miscreant to encrypt Rails session cookies. Some other interesting use cases are encrypting API tokens, passwords, database URLs, or other sensitive application configuration parameters, while still keeping the encrypted message size small.

Last but not least, I leave you with the “Key Rap” (a play on “key wrap”) from the very end of the original AES-SIV paper, which I’d like to dedicate all the chronic IV misusing miscreants in the land:

Yo! We’z gonna’ take them keys an’ whatever you pleaze
We gonna’ wrap ’em all up looks like some ran’om gup
Make somethin’ gnarly and funky won’t fool no half-wit junkie
So the game’s like AE but there’s one major hitch
No coins can be pitched there’s no state to enrich
the IV’s in a ditch dead drunk on cheap wine
Now NIST and X9 and their friends at the fort
suggest that you stick it in a six-layer torte
S/MIME has a scheme there’s even one more
So many ways that it’s hard to keep score
And maybe they work and maybe they’re fine
but I want some proofs for spendin’ my time
After wrappin’ them keys gonna’ help out some losers
chronic IV abusers don’t read no directions
risk a deadly infection If a rusty IV’s drippin’ into yo’ veins
and ya never do manage to get it exchanged
Then we got ya somethin’ and it comes at low cost
When you screw up again not all ’ill be lost